Finał 2007 Rozwiązania

Wysłane przez dn w pon., 14/09/2015 - 23:38

$ \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół średnich - Matematyka} \centerline{Finał VIII edycji - 28 kwietnia 2007} \centerline{Przykładowe rozwiązania} $

$\textbf{\underline{Zadanie 1.}} Znaleźć $\cos x$, jeśli wiadomo, że: $$\cos x\cdot\cos 2x=\cos 72^{\circ}\cdot\cos 36^{\circ}$$ \\ \\ \textbf{\underline{Rozwiązanie}} Obliczmy wartość wyrażenia $\cos 72^{\circ}\cdot\cos 36^{\circ}$, będziemy korzystać ze wzoru $\sin 2x=2\sin x\cos x$ oraz wzorów redukcyjnych: $$\cos 72^{\circ}\cdot\cos 36^{\circ}= \frac{\sin 36^{\circ}\cos 36^{\circ}\cos 72^{\circ}}{\sin 36^{\circ}}= \frac{\frac{1}{2}\sin 72^{\circ}\cos 72^{\circ}}{\sin 36^{\circ}}=$$ $$= \frac{\frac{1}{4}\sin 144^{\circ}}{\sin 36^{\circ}}= \frac{\sin (180^{\circ}-36^{\circ})}{4\sin 36^{\circ}}= \frac{\sin 36^{\circ}}{4\sin 36^{\circ}}= \frac{1}{4}$$ \\ Mamy więc równanie: $$\cos x\cos 2x=\frac{1}{4}$$ $$\cos x(2\cos^2x--1)=\frac{1}{4}$$ \\ Po podstawieniu $t=\cos x$ ($t\in\left<-1,1\right>$) należy znaleźć możliwe wartości $t$: $$t(2t^2-1)=\frac{1}{4}$$ $$4t(2t^2-1)=1$$ $$8t^3-4t-1=0$$ \\ Zauważamy, że $t=-\frac{1}{2}$ jest pierwiastkiem powyższego równania, stąd po podzieleniu wielomianu $8t^3-4t-1$ przez $t+\frac{1}{2}$, otrzymamy: $$(2t+1)(4t^2-2t-1)=0$$ \\ Stąd wyznaczamy wszystkie pierwiastki: $$t_1=-\frac{1}{2},\ t_2=\frac{1-\sqrt{5}}{2},\ t_3=\frac{1+\sqrt{5}}{2}$$ \\ Wszystkie znalezione pierwiastki należą do przedziału $\left<-1,1\right>$, stąd odpowiedź: $$\cos x\in\left\{-\frac{1}{2}, \frac{1-\sqrt{5}}{2}, \frac{1+\sqrt{5}}{2}\right\}$$ \\ \\ $

$\textbf{\underline{Zadanie 2.}} Trójkąt równoboczny $ABC$ wpisany jest w okrąg. Punkt $ K$ należy do mniejszego z łuków $ AB$ tego okręgu. Wykazać, że: $$|AK|+|BK|=|CK|$$ \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ $

$ \\ Niech $|AB|=|BC|=|CA|=a$, $|AK|=x$, $|KB|=y$, $|KC|=z$. \\ Chcemy udowodnić, że $x+y=z$. \\ Kąt $\angle AKC$ jest kątem wpisanym opartym na tym samym łuku co kąt wpisany $\angle ABC=60^{\circ}$, wobec czego $\angle AKC=60^{\circ}$. \\ Kąt $\angle CKB$ jest kątem wpisanym opartym na tym samym łuku co kąt wpisany $\angle CAB=60^{\circ}$, wobec czego $\angle CKB=60^{\circ}$. \\ Z tw. cosinusów dla trójkątów $AKC$ oraz $KBC$, otrzymujemy: $$\left\{\begin{array}{l} a^2=x^2+z^2-2xz\cos 60^{\circ} \\ a^2=y^2+z^2-2yz\cos 60^{\circ} \end{array}\right.$$ $$\left\{\begin{array}{l} a^2=x^2+z^2-xz \\ a^2=y^2+z^2-yz \end{array}\right.$$ \\ Po odcjęciu stronami: $$x^2-xz-y^2+yz=0$$ $$x^2-y^2-z(x-y)=0$$ $$(x-y)(x+y)-z(x-y)=0$$ $$(x-y)(x+y-z)=0$$ $$x=y\quad\vee\quad x+y=z$$ \\ Zatem pozostaje nam do rozważenia co się dzieje, gdy $x=y$. \\ Wtedy dcinek $CK$ jest średnicą okręgu i np. trójkąt $AKC$ to trójkąt prostokątny o kątach $\angle AKC=60^{\circ}$, $\angle KCA=30^{\circ}$, $\angle CAK=90^{\circ}$. Zachodzi zatem: $$|CK|=2|AK|$$ $$z=2x$$ $$z=x+x$$ $$z=x+y$$ \\ \\ $

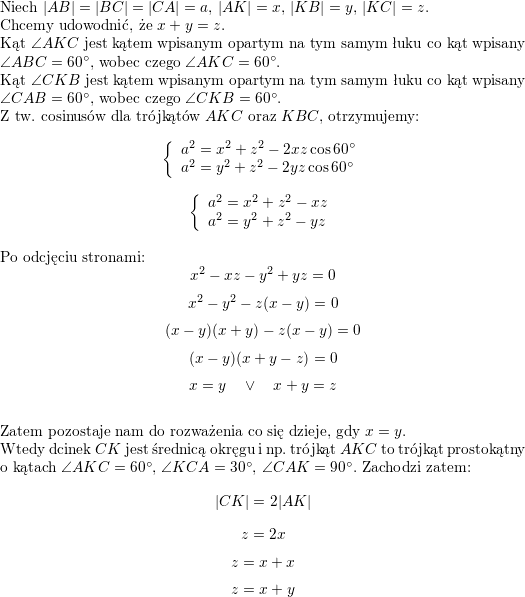
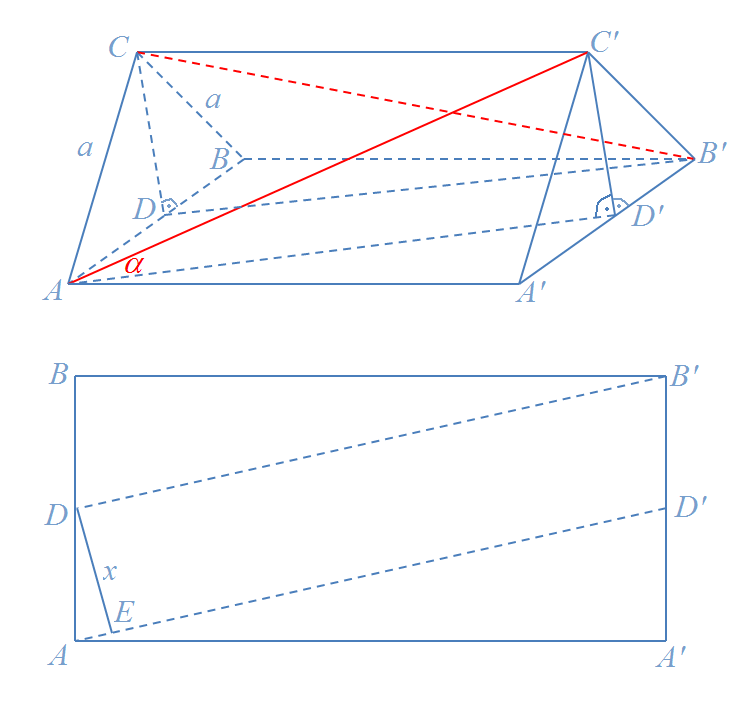
$\textbf{\underline{Zadanie 3.}} Obliczyć obwód trójkąta o wierzchołkach $ O\left( 0,0\right) $, $ A\left( \frac{3}{2}x_{0},0\right)$ i $ B$, jeśli $ x_{0}$ jest pierwiastkiem równania $$\displaystyle \left[ 3\left( 3^{\sqrt{x}+2}\right) ^{\frac{1}{\sqrt{x}}}\right]^{\frac{1}{\sqrt{x}-1}}=27$$ $B$ zaś punktem paraboli $$\displaystyle y=\frac{1}{2}x^{2}$$ którego odległość od punktu $ A$ jest najmniejsza. \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ Znajdźmy najpierw $x_0$. \\ Dziedziną równania w treści zadania jest zbiór $\mathbb{D}=(0,1)\cup(1,\infty)$: $$\left(3\cdot 3^{1+\frac{2}{\sqrt{x}}}\right)^{\frac{1}{\sqrt{x}-1}}=27$$ $$\left(3^{2+\frac{2}{\sqrt{x}}}\right)^{\frac{1}{\sqrt{x}-1}}=27$$ $$3^{\left(2+\frac{2}{\sqrt{x}}\right)\cdot\frac{1}{\sqrt{x}-1}}=3^3$$ \\ Z różnowartościowości funkcji wykładniczej: $$\left(2+\frac{2}{\sqrt{x}}\right)\cdot\frac{1}{\sqrt{x}-1}=3$$ \\ Podstawmy $t=\sqrt{x}$ ($t\in(0,1)\cup(\infty)$): \frac{2t+2}{t}\cdot\frac{1}{t-1}=3$$ $
$ $$2t+2=3t(t-1)$$ $$2t+2=3t^2-3t$$ $$3t^2-5t-2=0$$ $$(t-2)(3t+1)=0$$ $$t=2\quad\vee\quad t=-\frac{1}{3}$$ \\ Po uwzględnieniu z założeniami: $$t=2$$ $$\sqrt{x}=2$$ $$x=4$$ \\ Zatem $\displaystyle x_0=4$. \\ Ponadto punkt $A$ ma współrzędne $\left(6,0\right)$. \\ \\ Wyznaczymy teraz współrzędne punktu $B$. Skoro punkt ten leży na paraboli $y=\frac{1}{2}x^2$ to jego współrzędne możemy zapisać w postaci $B\left(b,\frac{1}{2}b^2\right)$ dla pewnej wartości $b\in\mathbb{R}$. \\ Musimy zatem znaleźć taką wartość $x$, dla której $d(A,B)$ osiąga wartość najmniejszą ($d(A,B)$ - odległość między punktami $A,B$). Możemy zapisać: $
$ $$d(A,B)= \sqrt{\left(x-6\right)^2+\left(\frac{1}{2}x^2-0\right)^2}= \sqrt{\frac{1}{4}x^4+x^2-12x+36}$$ \\ Ponieważ funkcja $\sqrt{x}$ jest rosnąca, to potrzebujemy znaleźć taki $x$ dla której funkcja $f(x)=\frac{1}{4}x^4+x^2-12x$ osiąga wartość najmniejszą. \\ Ponieważ $\displaystyle \lim_{x\to\pm\infty}f(x)=\infty$, oraz $f(x)$ jest wielomianem (funkcja ciągła dla której wszędzie istnieje $f'(x)$), to jej wartości najmniejszej poszukujemy wśród ekstremów lokalnych, czyli wartości dla których $f'(x)=0$. Warto zauważyć, że nie musimy stwierdzić w tym momencie jakim ekstremum (czy minimum, czy maksimum lokalnym) będzie znaleziony punkt dzięki równaniu $f'(x)=0$. Wystarczy policzyć wartości dla wszystkich $x$ dla których i wybrać tego $x$ dla którego otrzymamy najmniejszą wartość $f(x)$. Mianowicie: $$f'(x)=0$$ $$x^3+2x-12=0$$ $$(x-2)(x^2+2x+6)=0$$ $$x=2$$ \\ Dostaliśmy jedną wartość, więc $x=2$ musi być tym argumentem dla którego $f(x)$, więc i $d(A,B)$ przyjmuje wartość najmniejszą. \\ \\ Mamy obliczyć pole trójkąta o wierzchołkach w punktach $O(0,0), A(6,0), B(2,2)$, pole jest to zatem równe: $$P=\frac{1}{2}\cdot 6\cdot 2=6$$ \\ \\ $

$\textbf{\underline{Zadanie 4.}} Oddano serię $ n$ strzałów niezależnych od siebie. Prawdopodobieństwa chybienia celu w kolejnych strzałach równe są odpowiednio: $$\displaystyle \frac{1}{4},\frac{1}{9},\frac{1}{16},\ldots,\frac{1}{\left( n+1\right) ^{2}}.$$ Wykazać, że prawdopodobieństwo uzyskania serii $ n$ celnych strzałów równe jest $$\displaystyle \frac{n+2}{2\left( n+1\right) }.$$ \\ \\ \textbf{\underline{Rozwiązanie}} Skoro w $n$-tym strzale prawdopodobieństwo chybienia celu wynosi $p_n=\frac{1}{(n+1)^2}$, to ze wzoru na prawdopodobieństwo zdarzenia przeciwnego otrzymamy, że w $n$-tym strzale prawdopodobieństwo trafienia celu wynosi $$p_n'=1-p_n=1-\frac{1}{(n+1)^2}=\frac{n^2+2n+1-1}{(n+1)^2}= \frac{n(n+2)}{(n+1)(n+1)}$$ \\ Zatem prawdopodobieństwo serii $n$ celnych strzałów jest równe: $$p_1\cdot p_2\cdot p_3\cdot\ldots\cdot p_{n-2}\cdot p_{n-1}\cdot p_n=$$ $$= \frac{1\cdot 3}{2\cdot 2}\cdot\frac{2\cdot 4}{3\cdot 3}\cdot \frac{3\cdot 5}{4\cdot 4}\cdot\ldots\cdot \frac{(n-2)\cdot n}{(n-1)(n-1)}\cdot \frac{(n-1)(n+1)}{n\cdot n}\cdot \frac{n(n+2)}{(n+1)(n+1)}=$$ \\ Wszystko się prawie poskraca i zostanie: $$=\frac{1}{2}\cdot\frac{n+2}{n+1}= \frac{n+2}{2(n+1)}$$ \\ \\ $

$\textbf{\underline{Zadanie 5.}} W graniastosłupie prawidłowym trójkątnym o krawędzi podstawy długości $ a$, przekątna ściany bocznej tworzy z sąsiednią ścianą boczną kąt o mierze $ \alpha$. Jaka jest odległość między dwiema prostymi zawierającymi nieprzecinające się przekątne sąsiednich ścian bocznych tego graniastosłupa? \\ \\ \textbf{\underline{Rozwiązanie}} \\ \\ $

$ \\ Przyjmujemy oznaczenia takie jak na rysunku. Kąt $\alpha$ jest kątem w trójkącie prostokątnym $\Delta AD'C'$, oczywiście $D,D'$ to środki odpowiednio boków $AB,A'B'$. Zatem w trójkącie $\Delta AD'C'$ mamy zależność: $$\cot\alpha=\frac{|AD'|}{|C'D'|}$$ $$|AD'|=|C'D'|\cot\alpha=\frac{a\sqrt{3}}{2}\cot\alpha$$ \\ Niech $h$ oznacza długość wysokości graniastosłupa. \\ Następnie z tw. Pitagorasa w trójkącie $AA'D'$ otrzymujemy: $$|AA'|^2+|A'D'|^2=|AD'|^2$$ $$h^2+\left(\frac{a}{2}\right)^2=\frac{3a^2}{4}\cot^2\alpha$$ $$h^2=\frac{a^2}{4}\left(3\cot^2\alpha-1\right)$$ $$h=\frac{a}{2}\sqrt{3\cot^2\alpha-1}$$ \\ \\ Szukamy odległości między prostymi w których zawarte są odcinki $AC'$ oraz $B'C$. Gdy zrzutujemy te odcinki na płaszczyznę $AA'B'B$ otrzymamy odpowiednio odcinki $AD'$ oraz $B'D$. Ponieważ odcinki $AD'$ oraz $B'D$ są równoległe, to odległość między nimi (oznaczona przez $x$) będzie równa odległości między $AC'$ oraz $B'C$. \\ Z podobieństwa trójkątów $\Delta AED$ oraz $\Delta AA'D'$ (cecha: kkk) otrzymujemy: $$\frac{|DE|}{|AD|}=\frac{|AA'|}{|AD'|}$$ $$\frac{x}{\frac{a}{2}}=\frac{\frac{a}{2}\sqrt{3\cot^2\alpha-1}}{\frac{a\sqrt{3}}{2}\cot\alpha}$$ $$x=\frac{a\sqrt{3\cot^2\alpha-1}}{2\sqrt{3}\cot\alpha}$$ $