Finał 2004 Rozwiązania

Wysłane przez dn w pt., 08/05/2015 - 08:53

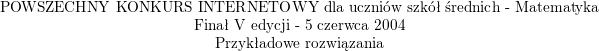
<br /> \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół<br /> średnich - Matematyka} \centerline{Finał V edycji - 5 czerwca 2004}<br /> \centerline{Przykładowe rozwiązania}<br />




\textbf{\underline{Zadanie 1.}} Ciąg $ \left( a_{n}\right) $ określony jest rekurencyjnie:<br /> $$\displaystyle a_{1}=\frac{1}{2},\ \displaystyle a_{n+1}=\sqrt{\frac{1+a_{n}}{2}}\ \ \mbox{dla}\ \ \displaystyle n=1,2,3,\ldots.$$<br /> Wykazać, że ten ciąg jest zbieżny i obliczyć jego granicę.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Udowodnimy, że ciąg $a_n$ jest ograniczony z góry przez $1$.<br /> \\ Skorzystamy z metody indukcji matematycznej, sprawdzamy dla $n=1$, otrzymujemy, że $a_1=\frac{1}{2}<1$, jest w porządku.<br /> \\ Założenie indukcyjne: $a_n<1$, chcemy pokazać tezę indukcyjną, tzn. $a_{n+1}<1$.<br /> \\ Z definicji rekurencyjnej otrzymujemy zależność:<br /> $$a_{n+1}=\frac{a_n+1}{2}$$<br /> Korzystając z założenia indukcyjnego, otrzymujemy:<br /> $$a_{n+1}<\frac{1+1}{2}=1$$<br /> \\ Zatem na mocy indukcji matematycznej udowodniliśmy, że ciąg $a_n$ jest ograniczony z góry przez $1$.<br /> \\<br /> \\ Sprawdźmy monotoniczność ciągu $a_n$, badając znak różnicy jego dwóch kolejnych wyrazów:<br /> $$a_{n+1}-a_n=\frac{1+a_n}{2}-a_n=<br /> \frac{1+a_n-2a_n}{2}=<br /> \frac{1-a_n}{2}$$<br /> \\ Ponieważ $a_n<1$, to $1-a_n>0$, więc $a_{n+1}-a_n>0$, czyli uzasadniliśmy, żę ciąg $a_n$ jest ciągiem rosnącym.<br /> \\<br /> \\ Ponieważ ciąg $a_n$ jest ciągiem rosnącym i ograniczonym z góry, to jest zbieżny. Oznaczmy jego granicę przez $A$.<br /> \\ Przechodząc w zależności rekurencyjnej do granicy przy $n\to\infty$, otrzymujemy:<br /> $$\lim_{n\to\infty}a_{n+1}=\lim_{n\to\infty}\frac{1+a_n}{2}$$<br /> $$A=\frac{1+A}{2}$$<br /> $$2A=1+A$$<br /> $$A=1$$<br /> \\ Zatem pokazaliśmy, że:<br /> $$\lim_{n\to\infty}a_n=1$$<br /> \\ \\<br />

\textbf{\underline{Zadanie 2.}} Wykazać, że w trójkącie prostokątnym dwusieczna kąta prostego jest jednocześnie dwusieczną kąta między środkową i wysokością tego trójkąta opuszczonymi z wierzchołka kąta prostego.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br />

<br /> \\ Przyjmijmy oznaczenia jak na rysunku, mamy trójkąt $ABC$ z kątem prostym przy wierzchołku $A$, punkt $D$ jest spodkiem wysokości opuszczonej na przeciwprostokątną, $E$ jest punktem przecięcia się dwusiecznej kąta $\angle CAB$ z przeciwprostokątną, punkt $F$ jest środkiem przeciwprostokątnej, punkt $G$ jest rzutem prostokątnym punktu $F$ na bok $AB$.<br /> \\ \\<br /> Przyjmijmy dodatkowo, że $\angle FAG=\alpha$, ponieważ $F$ jest również środkiem okręgu opisanego na trójkącie, to oczywiście $|AF|=|FB|$ i stąd otrzymamy, że $\angle FBG=\alpha$, wtedy z sumy miar kątów wewnętrznych w trójkącie $ABC$ mamy zależność: $\angle ACB=90^{\circ}-\alpha$, wtedy z sumy miar kątów wewnętrznych w trójkącie $ADC$ otrzymujemy, że $\angle CAD=90^{\circ}-(90^{\circ}-\alpha)=\alpha$.<br /> \\ Ponieważ $AE$ zawiera się w dwusiecznej kąta prostego $CAB$, to $\angle CAE=\angle EAB=45^{\circ}$, zatem:<br /> $$\angle DAE=\angle CAE-\angle CAD=45^{\circ}-\alpha$$<br /> $$\angle EAF=\angle EAB-\angle FAB=45^{\circ}-\alpha$$<br /> \\ Zatem rzeczywiście odcinek $AE$ jest dwusieczną kąta $\angle DAF$, co należało wykazać.<br /> \\ \\<br />

\textbf{\underline{Zadanie 3.}} Wyznaczyć zbiór wszystkich rzeczywistych wartości parametru $ k$, dla których pierwiastki wielomianu<br /> $$\displaystyle W\left( x\right) =\frac{1}{3}x^{3}-\frac{3k}{2}x^{2}+2k^{2}x-k$$<br /> są długościami krawędzi prostopadłościanu, którego żadna ściana nie jest kwadratem. \\<br /> Dla takich wartości $ k$ wyznaczyć pole powierzchni całkowitej tego prostopadłościanu.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Niech $x_1,x_2,x_3$ będą pierwiastkami równania. By warunki zadania były spełnione liczby $x_1,x_2,x_3$ muszą być parami różnymi dodatnimi liczbami.<br /> \\ Ze wzorów Viete'y dla wielomianu trzeciego stopnia otrtzymujemy:<br /> $$x_1+x_2+x_3=\frac{\frac{3k}{2}}{\frac{1}{3}}=\frac{9k}{2}$$<br /> $$x_1x_2+x_1x_3+x_2x_3=\frac{2k^2}{\frac{1}{3}}=6k^2$$<br /> $$x_1x_2x_3=\frac{k}{\frac{1}{3}}=3k$$<br /> \\ Zatem na pewno musi zachodzić $k>0$.<br />
<br /> \\<br /> $$W'(x)=x^2-3kx+2k^2=(x-2k)(x-k)$$<br /> \\ $W'(x)>0$ dla $x\in(-\infty,k)$ oraz dla $x\in(2k,\infty)$, więc w tych przedziałach $W(x)$ rośnie,<br /> $W'(x)<0$ dla $x\in(k,2k)$, więc w tych przedziałach $W(x)$ maleje, stąd wynika, że dla $x=k$ otrzymujemy maksimum lokalne a dla $x=2k$ otrzymujemy minimum lokalne.<br /> \\<br /> \\ Oczywiście $\displaystyle \lim_{x\to\infty}W(x)=\infty$.<br /> \\ By $W(x)$ miał trzy dodatnie różne rozwiązania, to musi zachodzić, że $W(0)<0$ (zachodzi) oraz $W(k)>0$ oraz $W(2k)<0$, bo wtedy w każdym z przedziałów $(0,k)$, $(k,2k)$, $(2k,\infty)$ będzie znajdował się dokładnie jeden pierwiastek wyjściowego równania.<br /> \\ Liczymy zatem:<br /> $$W(k)>0$$<br /> $$\frac{1}{3}k^3-\frac{3k}{2}\cdot k^2+2k^2\cdot k-k>0$$<br /> $$\frac{1}{3}k^3-\frac{3k^3}{2}+2k^3-k>0$$<br /> $$2k^3-9k^3+12k^3-6k>0$$<br /> $$5k^3-6k>0$$<br /> $$5k\left(k^2-\frac{6}{5}\right)>0$$<br /> \\ Ponieważ $k>0$:<br /> $$k^2-\frac{6}{5}>0$$<br /> $$k^2>\frac{6}{5}$$<br /> $$|k|>\sqrt{\frac{6}{5}}$$<br /> $$k>\sqrt{\frac{6}{5}}$$<br /> \\ Teraz:<br />
<br /> $$W(2k)<0$$<br /> $$\frac{1}{3}8k^3-\frac{3k}{2}\cdot 4k^2+2k^2\cdot 2k-k<0$$<br /> $$\frac{8}{3}k^3-6k^3+4k^3-k<0$$<br /> $$\frac{8}{3}k^3-2k^2-k<0$$<br /> $$8k^3-6k^3-3k<0$$<br /> $$2k^3-3k<0$$<br /> $$2k\left(k^2-\frac{3}{2}\right)<0$$<br /> $$k^2<\frac{3}{2}$$<br /> $$|k|<\sqrt{\frac{3}{2}}$$<br /> $$k<\sqrt{\frac{3}{2}}$$<br /> \\<br /> Zatem:<br /> $$k\in\left(\sqrt{\frac{6}{5}},\sqrt{\frac{3}{2}}\right)$$<br /> \\ Ze wzorów Viete pole powierzchni całkowitej jest równe:<br /> $$P_c=2(x_1x_2+x_1x_3+x_2x_3)=2\cdot 6k^2=12k^2$$<br /> \\ \\<br />

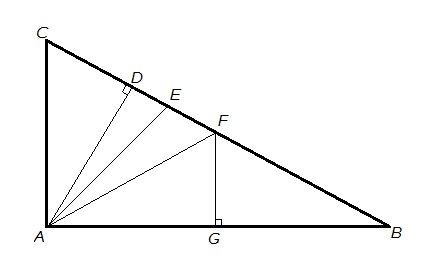
\textbf{\underline{Zadanie 4.}} Obliczyć jednostronną granicę<br /> $$\displaystyle \lim_{x\rightarrow\pi^{-}}\left[ \left( x-\pi\right) \left(\cot x\cdot\sqrt{\cot^2x-\cot x+1}+\cot^2x\right)\right]$$<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Podstawmy $x-\pi=t$, wtedy $\cot x=\cot(t+\pi)=\cot t$ oraz liczymy:<br /> $$\lim_{t\to 0^-}t\cot t\left(\sqrt{\cot^2t-\cot t+1}+\cot t}\right)=$$<br /> \\ Ze wzoru $a+b=\frac{a^2-b^2}{a-b}$:<br /> $$=<br /> \lim_{t\to 0^-} t\cot t\cdot\frac{\cot^2t-\cot t+1-\cot^2t}{\sqrt{\cot^2t-\cot t+1}-\cot t}=$$ $$=<br /> \lim_{t\to 0^-} t\cdot\frac{\cos t}{\sin t}\cdot\frac{-\cot t+1}{|\cot t|\sqrt{1-\tan t+\tan^2t}-\cot t}=$$ $$=<br /> \lim_{t\to 0^-}\frac{\cos t}{\displaystyle\frac{\sin t}{t}}\cdot\frac{\cot t(-1+\tan t)}{-\cot t\sqrt{1-\tan t+\tan^2t}-\cot t}=$$ $$<br /> \lim_{t\to 0^-}\frac{\cos t}{\displaystyle\frac{\sin t}{t}}\cdot\frac{-1+\tan t}{-\sqrt{1-\tan t+\tan^2t}-1}=$$<br /> \\ Korzystamy teraz ze znanej granicy $\displaystyle \lim_{\alpha\to 0}\frac{\sin\alpha}{\alpha}=1$, otrzymując:<br /> $$=\frac{1}{1}\cdot\frac{-1+0}{-\sqrt{1-0+0}-1}=\frac{1}{2}$$<br /> \\ \\<br />

\textbf{\underline{Zadanie 5.}} Rzucamy symetryczną sześcienną kostką do gry tak długo, aż wyrzucimy kolejno dwie szóstki. Możemy wykonać maksymalnie 6 rzutów. Jakie jest prawdopodobieństwo zdarzenia polegającego na tym, że będziemy rzucać kostką 6 razy?<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Obliczyć jednostronnÄ… granicÄ™<br /> $$\displaystyle \lim_{x\rightarrow\pi^{-}}\left[ \left( x-\pi\right) \left(\cot x\cdot\sqrt{\cot^2x-\cot x+1}+\cot^2x\right)\right].$$<br /> \\ \\<br /> \textbf{\underline{RozwiÄ…zanie}}<br /> Podstawmy $x-\pi=t$, wtedy $\cot x=\cot(t+\pi)=\cot t$ oraz nasza poczÄ…tkowa granica jest rĂłwna:<br /> \begin{align*}<br /> \lim_{t\to 0^-} & t\cot t\left(\sqrt{\cot^2t-\cot t+1}+\cot t\right) =\\<br /> &=\lim_{t\to 0^-} t\cot t\cdot\frac{\cot^2t-\cot t+1-\cot^2t}{\sqrt{\cot^2t-\cot t+1}-\cot t}\\<br /> &=\lim_{t\to 0^-} t\cdot\frac{\cos t}{\sin t}\cdot\frac{-\cot t+1}{|\cot t|\sqrt{1-\tan t+\tan^2t}-\cot t}\\<br /> &=\lim_{t\to 0^-}\frac{\cos t}{\displaystyle\frac{\sin t}{t}}\cdot\frac{\cot t(-1+\tan t)}{-\cot t\sqrt{1-\tan t+\tan^2t}-\cot t}\\<br /> &=\lim_{t\to 0^-}\frac{\cos t}{\displaystyle\frac{\sin t}{t}}\cdot\frac{-1+\tan t}{-\sqrt{1-\tan t+\tan^2t}-1}\\<br /> &=\frac{1}{1}\cdot\frac{-1+0}{-\sqrt{1-0+0}-1}\\<br /> &=\frac{1}{2}<br /> \end{align*}<br /> \\ KorzystaliĹ›my ze znanej granicy $\displaystyle \lim_{\alpha\to 0}\frac{\sin\alpha}{\alpha}=1$.<br /> \\ \\<br /> \textbf{\underline{Zadanie 5.}} Zauważmy na początek, że szansa wyrzucenia $6$ wynosi $\displaystyle\frac{1}{6}$, a szansa wylosowania nie szóstki $\displaystyle\frac{5}{6}$. Niech $\not 6$ oznacza, że w ciągu rzutów wyrzuciliśmy nie szóstkę. Wtedy, rozpisując wszystkie możliwe sytuacje, otrzymujemy, że jedynymi możliwymi ciągami rzutów są (niech $p_i$ oznacza prawdopodobieństwo otrzymania $i$-tego ciągu rzutów kostką):<br /> <br /> \begin{enumerate}<br /> \item \begin{tabular}{|c|c|c|c|c|c|}\hline<br /> 6&$\not 6$&6&$\not 6$&6&6 \\ \hline \end{tabular}, $\displaystyle p_1=\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{25}{6^6},$<br /> \\<br /> \item \begin{tabular}{|c|c|c|c|c|c|}\hline<br /> 6&$\not 6$&$\not 6$&$\not 6$&6&6 \\ \hline \end{tabular}, $\displaystyle p_1=\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{125}{6^6},$<br /> \\<br /> \item \begin{tabular}{|c|c|c|c|c|c|}\hline<br /> $\not 6$&6&$\not 6$&$\not 6$&6&6 \\ \hline \end{tabular}, $\displaystyle p_1=\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{125}{6^6},$<br /> \\<br /> \item \begin{tabular}{|c|c|c|c|c|c|}\hline<br /> $\not 6$&$\not 6$&6&$\not 6$&6&6 \\ \hline \end{tabular}, $\displaystyle p_1=\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{125}{6^6},$<br /> \\<br /> \item \begin{tabular}{|c|c|c|c|c|c|}\hline<br /> $\not 6$&$\not 6$&$\not 6$&$\not 6$&6&6 \\ \hline \end{tabular}, $\displaystyle p_1=\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{5}{6}\cdot\frac{1}{6}\cdot\frac{1}{6}=\frac{625}{6^6}.$<br /> \end{enumerate}<br /> Stąd szukane prawdopodobieństwo jest równe:<br /> \begin{align*}<br /> p<br /> &=p_1+p_2+p_3+p_4+p_5+p_6 \\<br /> &=\frac{25}{6^6}+\frac{125}{6^6}+\frac{125}{6^6}+\frac{125}{6^6}+\frac{625}{6^6}\\<br /> &=\frac{1025}{6^6}.<br /> \end{align*}<br /> \\ \\<br />

<br /> \centerline{\bf Za rozwiązanie każdego zadania można uzyskać<br /> maksymalnie 20 punktów}<br />