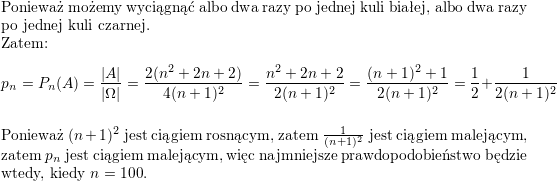Finał 2003 Rozwiązania

Wysłane przez dn w czw., 07/05/2015 - 11:38

<br /> \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół<br /> średnich - Matematyka} \centerline{Finał IV edycji - 14 czerwca 2003}<br /> \centerline{Przykładowe rozwiązania}<br />




\textbf{\underline{Zadanie 1.}} Niech $ A$ będzie zbiorem rozwiązań na przedziale $ \left\langle 0;2\pi\right\rangle $ równania<br /> $$\displaystyle \cos x-\sin x+\sin2x=1$$<br /> i odpowiednio $ B$ zbiorem rozwiązań na przedziale $ \left\langle 0;2\pi\right\rangle $ równania<br /> $$\operatorname*{tg}x-\operatorname*{tg}\left( x-\frac{\pi}{3}\right)=\sqrt{3}.$$<br /> Znaleźć iloczyn $ A\cap B$ i sumę $ A\cup B$.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> W pierwszym równaniu zauważmy, że<br /> \\<br /> $\sin 2x=2\sin x\cos x=-(1-2\sin x\cos x)+1=<br /> 1-(\cos x-\sin x)^2$, po podstawieniu $t=\cos x-\sin x$, otrzymujemy:<br /> $$t+1-t^2=1$$<br /> $$t(1-t)=0$$<br /> $$t=0\quad\vee\quad t=1$$<br /> $$\cos x-\sin x=0\quad\vee\quad \cos x-\sin x=1$$<br /> $$\cos x=\sin x\quad\vee\quad \frac{1}{\sqrt{2}}\cos x-\frac{1}{\sqrt{2}}\sin x=\frac{1}{\sqrt{2}}$$<br /> $$\cos x=\cos\left(\frac{\pi}{2}-x\right)\quad\vee\quad \cos\frac{\pi}{4}\cos x-\sin\frac{\pi}{4}\sin x=\frac{\sqrt{2}}{2}$$<br />
<br /> $$\cos x=\cos\left(\frac{\pi}{2}-x\right)\quad\vee\quad \cos\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}$$<br /> $$x=\frac{\pi}{2}-x+2k\pi\quad\vee\quad x=-\frac{\pi}{2}+x+2k\pi\quad\vee\quad x+\frac{\pi}{4}=\frac{\pi}{4}+2k\pi\quad\vee\quad x+\frac{\pi}{4}=-\frac{\pi}{4}+2k\pi,\ \ k\in\mathbb{Z}$$<br /> $$x=\frac{\pi}{4}+k\pi\quad\vee\quad x=2k\pi\quad\vee\quad x=-\frac{\pi}{2}+2k\pi$$<br /> \\ Zatem:<br /> $$A=\left\{\frac{\pi}{4},\frac{5\pi}{4},0,2\pi, \frac{3\pi}{2}\right\}$$<br /> \\ \\ Zajmijmy się drugim równaniem.<br /> \\ Dziedzina tego równania to $x\neq\frac{\pi}{2}+ k\pi$ oraz $x\neq\frac{\pi}{3}+\frac{\pi}{2}+k\pi$ dla $k\in\mathbb{Z}$.<br /> \\ Dalej skorzystamy ze wzoru $\displaystyle \tan(a-b)=\frac{\tan a-\tan b}{1+\tan a\tan b}$:<br /> $$\tan x-\frac{\tan x-\tan\frac{\pi}{3}}{1+\tan x\tan\frac{\pi}{3}}=\sqrt{3}$$<br /> \\ Podstawmy $t=\tan x$:<br /> $$t-\frac{t-\sqrt{3}}{1+\sqrt{3}t}=\sqrt{3}$$<br /> $$t(1+\sqrt{3}t)-t+\sqrt{3}=\sqrt{3}(1+\sqrt{3}t)$$<br /> $$t+\sqrt{3}t^2-t+\sqrt{3}=\sqrt{3}+3t$$<br /> $$\sqrt{3}t^2-3t=0$$<br /> $$\sqrt{3}t(t-\sqrt{3})=0$$<br />
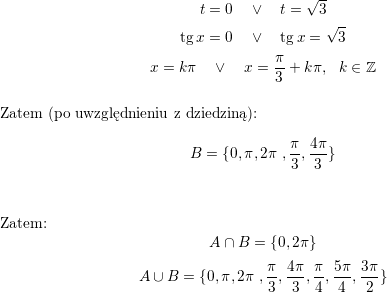
<br /> $$t=0\quad\vee\quad t=\sqrt{3}$$<br /> $$\tan x=0\quad\vee\quad\tan x=\sqrt{3}$$<br /> $$x=k\pi\quad\vee\quad x=\frac{\pi}{3}+k\pi,\ \ k\in\mathbb{Z}$$<br /> \\ Zatem (po uwzględnieniu z dziedziną):<br /> $$B=\left\{0,\pi,2\pi\right,\frac{\pi}{3},\frac{4\pi}{3}\}$$<br /> \\ \\ Zatem:<br /> $$A\cap B=\left\{0,2\pi\right\}$$<br /> $$A\cup B=\left\{0,\pi,2\pi\right,\frac{\pi}{3},\frac{4\pi}{3},\frac{\pi}{4},\frac{5\pi}{4},\frac{3\pi}{2}\}$$<br /> \\ \\<br />

\textbf{\underline{Zadanie 2.}} Dany jest trójkąt ostrokątny ABC. Punkty D, E, F są odpowiednio środkami boków AB, BC, AC, zaś punkt G jest spodkiem wysokości trójkąta opuszczonej z wierzchołka C. Wykaż, że punkty D, E, F, G leżą na okręgu.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br />

<br /> Oczywiście odcinek $FE$ (łączący środki boków $AC$, $BC$) jest równoległy do $AB$, stąd:<br /> $$\angle FDE=\angle AFD=\angle ACB$$<br /> \\ Ponieważ punkty $E$ i $F$ są środkami boków, to zachodzą ponadto równości $|CF|=|FG|$ oraz $|CE|=|CG|$, stąd otrzymujemy:<br /> $$\angle FGE=\angle FGC+\angle EGC=\angle FCG+\angle ECG=\angle FCE=\angle FDE$$<br /> \\ Zatem punkt $G$ leży na okręgu opisanych na trójkącie $FED$, czyli punkty $D,E,F,G$ leżą na jednym okręgu.<br /> \\ \\<br />

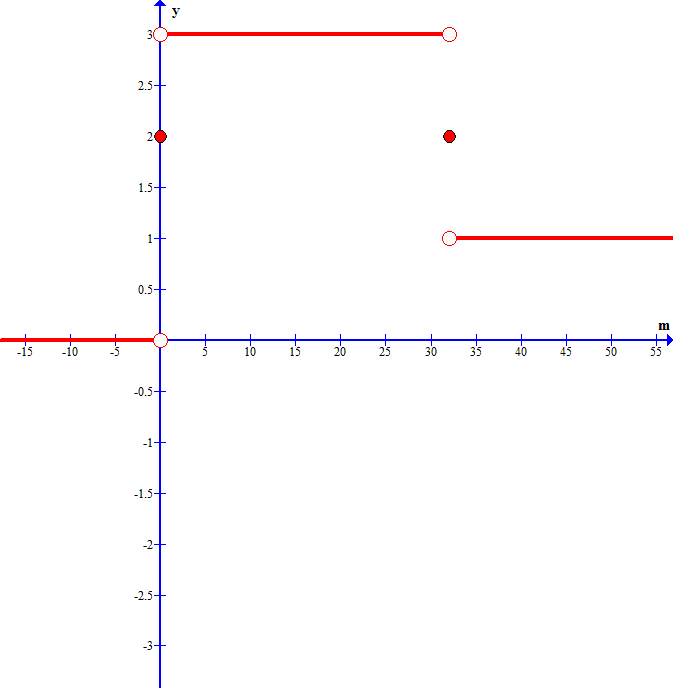
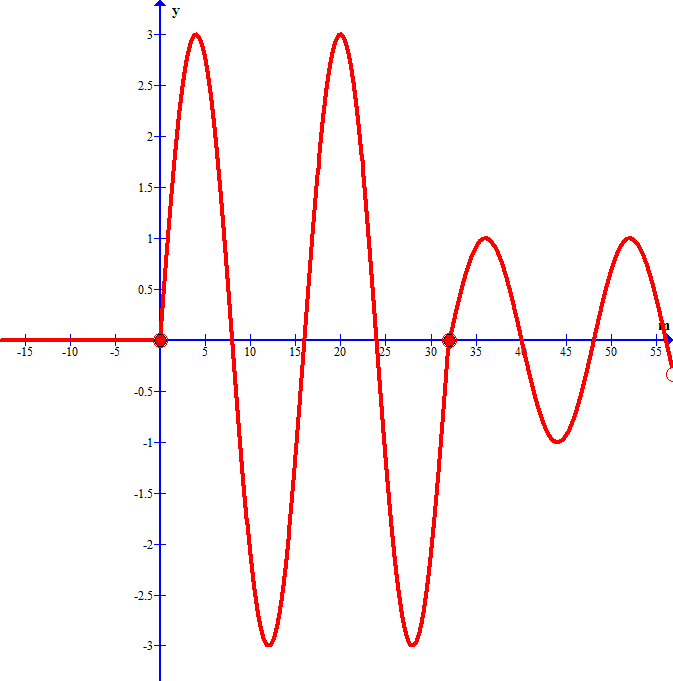
\textbf{\underline{Zadanie 3.}} Funkcja $ l\left( m\right) $ przyporządkowuje argumentowi rzeczywistemu $ m$ liczbę rozwiązań równania$ \left[ f\left( x\right) \right] ^{2}=m$, gdzie<br /> $$\displaystyle f\left( x\right) =\sqrt{x^{3}-12x+16}.$$<br /> Funkcja $ h\left( m\right) $ określona jest wzorem<br /> $$\displaystyle h\left( m\right) =l\left( m\right) \sin\left( \frac{\pi}{8}m\right).$$<br /> Zbadać ciągłość i różniczkowalność oraz wyznaczyć ekstrema funkcji $ h\left( m\right) $. 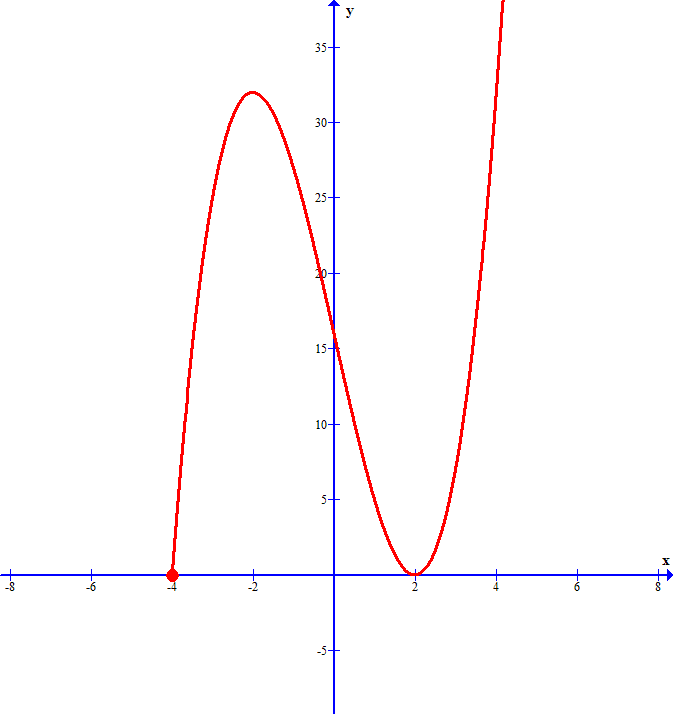Narysować wykres tej funkcji.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Wyznaczmy najpierw dziedzinę funkcji $f$, musi więc zachodzić:<br /> $$x^3-12x+16\geqslant 0$$<br /> $$(x-2)^2(x+4)\geqslant 0$$<br /> $$x\in\left<-4,\infty\right)$$<br /> \\ \\ Naszkicujmy teraz wykres funkcji $M(x)=[f(x)^2]=x^3-12x+16$ dla $x\in\left<-4,\infty\right)$.<br /> \\ Skoro $M(x)=(x-2)^2(x+4)$ to miejscami zerowymi są oczywiście $2$ oraz $-4$.<br /> \\ Wyznaczmy ekstrema:<br /> $$M'(x)=3x^2-12=3(x-2)(x+2)$$<br /> \\ $M'(x)>0$ zachodzi dla $x\in(0,2)$ oraz dla $x\in(4,\infty)$ i w tych przedziałach funkcja $M$ rośnie,<br /> a $M'(x)<0$ zachodzi dla $x\in(2,4)$ zatem w tym przedziale funkcja $M(x)$ maleje.<br />
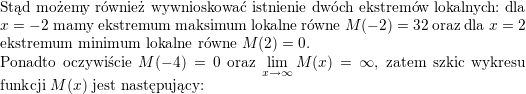
<br /> \\ Stąd możemy również wywnioskować istnienie dwóch ekstremów lokalnych: dla $x=-2$ mamy ekstremum maksimum lokalne równe $M(-2)=32$ oraz dla $x=2$ ekstremum minimum lokalne równe $M(2)=0$.<br /> \\ Ponadto oczywiście $M(-4)=0$ oraz $\displaystyle \lim_{x\to\infty}M(x)=\infty$, zatem szkic wykresu funkcji $M(x)$ jest następujący:<br />

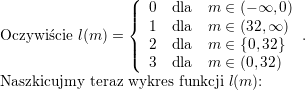
<br /> \\ Oczywiście $l(m)=\left\{\begin{array}{lll}<br /> 0 & \mbox{dla} & m\in(-\infty,0) \\<br /> 1 & \mbox{dla} & m\in(32,\infty) \\<br /> 2 & \mbox{dla} & m\in\{0,32\} \\<br /> 3 & \mbox{dla} & m\in(0,32)\end{array}\right.$.<br /> \\ Naszkicujmy teraz wykres funkcji $l(m)$:<br /> \\

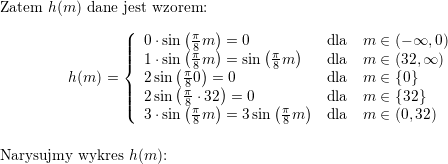
<br /> \\ \\ Zatem $h(m)$ dane jest wzorem:<br /> $$h(m)=\left\{\begin{array}{lll}<br /> 0\cdot\sin\left(\frac{\pi}{8}m\right)=0 & \mbox{dla} & m\in(-\infty,0) \\<br /> 1\cdot \sin\left(\frac{\pi}{8}m\right)=\sin\left(\frac{\pi}{8}m\right) & \mbox{dla} & m\in(32,\infty) \\<br /> 2\sin\left(\frac{\pi}{8}0\right)=0 & \mbox{dla} & m\in\{0\} \\<br /> 2\sin\left(\frac{\pi}{8}\cdot 32\right)=0 & \mbox{dla} & m\in\{32\} \\<br /> 3\cdot\sin\left(\frac{\pi}{8}m\right)=3\sin\left(\frac{\pi}{8}m\right) & \mbox{dla} & m\in(0,32)\end{array}\right.$$<br /> \\ Narysujmy wykres $h(m)$:<br />

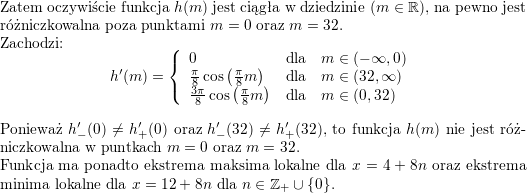
<br /> \\ Zatem oczywiście funkcja $h(m)$ jest ciągła w dziedzinie ($m\in\mathbb{R}$),<br /> na pewno jest różniczkowalna poza punktami $m=0$ oraz $m=32$.<br /> \\ Zachodzi:<br /> $$h'(m)=\left\{\begin{array}{lll}<br /> 0 & \mbox{dla} & m\in(-\infty,0) \\<br /> \frac{\pi}{8}\cos\left(\frac{\pi}{8}m\right) & \mbox{dla} & m\in(32,\infty) \\<br /> \frac{3\pi}{8}\cos\left(\frac{\pi}{8}m\right) & \mbox{dla} & m\in(0,32)\end{array}\right.$$<br /> \\ Ponieważ $h'_-(0)\neq h'_+(0)$ oraz $h'_-(32)\neq h'_+(32)$, to funkcja $h(m)$ nie jest różniczkowalna w puntkach $m=0$ oraz $m=32$.<br /> \\ Funkcja ma ponadto ekstrema maksima lokalne dla $x=4+8n$ oraz ekstrema minima lokalne dla $x=12+8n$ dla $n\in\mathbb{Z}_+\cup\{0\}$.<br />

\textbf{\underline{Zadanie 4.}} Obliczyć granicę ciągu $ \left(a_{n}\right) $, gdzie<br /> $$\displaystyle a_{n}=n\cos\left( \pi n\right) \cos\left( \pi\sqrt{n^{2}+1}\right)\sin\frac{1}{n}.$$<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Na początek zauważmy, że $\cos(\pi n)=(-1)^n$, i wtedy ze wzorów redukcyjnych $(-1)^n\cos\left(\pi\sqrt{1+n^2}\right)=<br /> \cos\left(\pi\sqrt{n^2+1}-n\pi\right)$. Zatem:<br /> $$\lim_{n\to\infty} a_n=$$ $$=<br /> \lim_{n\to\infty} \cos\left[\pi\left(\sqrt{n^2+1}-n\right)\right]\cdot\frac{\sin\frac{1}{n}}{\frac{1}{n}}=$$ $$=<br /> \lim_{n\to\infty} \cos\left(\pi\cdot\frac{n^2+1-n^2}{\sqrt{n^2+1}+n}\right)\cdot\frac{\sin\frac{1}{n}}{\frac{1}{n}}=$$ $$=<br /> \lim_{n\to\infty} \cos\left(\pi\cdot\frac{1}{\sqrt{n^2+1}+n}\right)\cdot\frac{\sin\frac{1}{n}}{\frac{1}{n}}=$$<br /> \\ Skorzystamy teraz ze znanej granicy $\displaystyle \lim_{\alpha\to 0}\frac{\sin\alpha}{\alpha}=1$, więc otrzymujemy:<br /> $$=\left[\cos\left(\pi\cdot\frac{1}{\infty}\right)\cdot 1=\cos 0\cdot 1\right]=1\cdot 1=1$$<br /> \\ \\<br />

\textbf{\underline{Zadanie 5.}} W urnie jest n kul białych i o dwie więcej kul czarnych. Losujemy dwukrotnie ze zwracaniem po jednej kuli. Dla jakiego n ze zbioru $\{0,1,...,100\}$ prawdopodobieństwo zdarzenia: wylosowano dwie kule jednego koloru, jest najmniejsze?<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Zatem kulek czarnych jest $n+2$.<br /> \\ Niech $\Omega$ oznacza przestrzeń wszystkich zdarzeń elementarnych polegających na wyciągnięciu z danej urny dwóch ze zwracaniem, ponieważ wszystkich kul w urnie jest $n+n+2=2n+2$, to:<br /> $$|\Omega|=(2n+2)(2n+2)=4(n+1)^2$$<br /> \\ Niech $A$ oznacza zbiór zdarzeń elementarnych polegających na wyciągnięciu z urny dwóch kul tego samego koloru. Zatem:<br /> $$|A|=n\cdot n+(n+2)(n+2)=2n^2+4n+4$$<br />
<br /> \\ Ponieważ możemy wyciągnąć albo dwa razy po jednej kuli białej, albo dwa razy po jednej kuli czarnej.<br /> \\ Zatem:<br /> $$p_n=P_n(A)=\frac{|A|}{|\Omega|}=\frac{2(n^2+2n+2)}{4(n+1)^2}=<br /> \frac{n^2+2n+2}{2(n+1)^2}=<br /> \frac{(n+1)^2+1}{2(n+1)^2}=<br /> \frac{1}{2}+\frac{1}{2(n+1)^2}$$<br /> \\ Ponieważ $(n+1)^2$ jest ciągiem rosnącym, zatem $\frac{1}{(n+1)^2}$ jest ciągiem malejącym, zatem $p_n$ jest ciągiem malejącym, więc najmniejsze prawdopodobieństwo będzie wtedy, kiedy $n=100$.<br /> \\ \\<br />
<br /> \centerline{\bf Za rozwiązanie każdego zadania można uzyskać<br /> maksymalnie 20 punktów}<br />