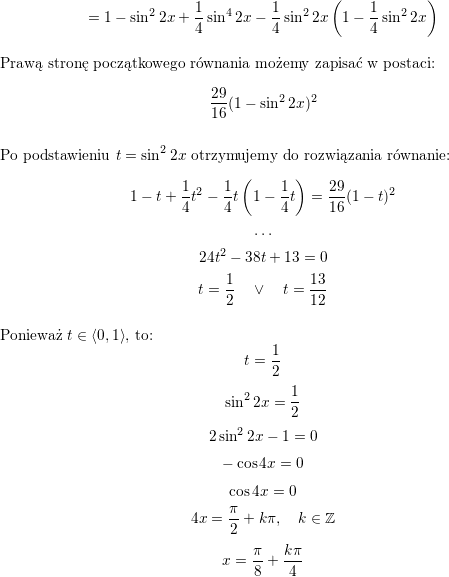Jesteś tutaj
Organizatorzy konkursu
Patroni Konkursu
Kontakt Elektroniczny
sprawy techniczne:
konkurs_strona[at]mini.pw.edu.pl.
sprawy merytoryczne:
konkurs_uwagi[at]mini.pw.edu.pl.
reklamacje:
konkurs_odwolania[at]mini.pw.edu.pl.
Deklaracja Dostępności
Adres pocztowy
WYDZIAŁ MATEMATYKI I NAUK INFORMACYJNYCH POLITECHNIKI WARSZAWSKIEJ ul. Koszykowa 75, 00-662 WARSZAWA, pokój 17,
dopisek KONKURS
Wszystkie prawa zastrzeżone © 1999-2025 Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej
Stronę napędza Drupal


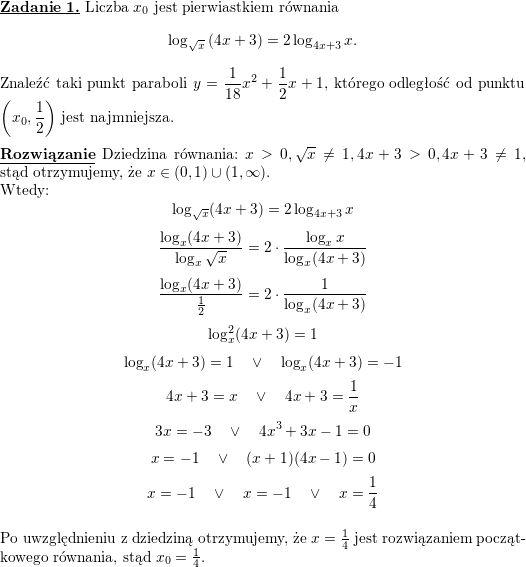
![<br />
\\ \\<br />
Niech szukanym punktem będzie $B\left(m,\frac{1}{18}m^2+\frac{1}{2}m+1\right)$.<br />
\\ Dodatkowo $A\left(\frac{1}{4},\frac{1}{2}\right)$.<br />
\\ Zauważmy, że wtedy styczna do paraboli w punkcie $B$ będzie prostopadła<br />
do wektora $\overrightarrow{AB}=\left[m-\frac{1}{4},\frac{1}{18}m^2+\frac{1}{2}m+\frac{1}{2}\right]$.<br />
\\ Ponieważ $y'=\frac{x}{9}+\frac{1}{2}$, to styczna w punkcie $B$ będzie miała współczynnik kierunkowy $\frac{m}{9}+\frac{1}{2}$, więc wektorem równoległym do stycznej będzie np. wektor $\vec v=\left[1,\frac{m}{9}+\frac{1}{2}\right]$, przeskalujmy go przez $18$: $\vec w=\left[18,2m+9\right]$.<br />
\\ Zatem ma zachodzić:<br />
$$\vec v\perp\overrightarrow{AB}$$<br />
$$\vec v\circ\overrightarrow{AB}=0$$<br />
$$\left(m-\frac{1}{4}\right)\cdot 18+\left(\frac{1}{18}m^2+\frac{1}{2}m+\frac{1}{2}\right)(2m+9)=0$$<br />
$$\ldots$$<br />
$$m(2m^2+27m+423)=0$$<br />
\\ Jedynym rozwiązaniem jest $m=0$, zatem szukanym punktem jest<br />
$$B\left(0,1\right)$$<br />
\\ \\<br />](/files/tex/c6dad43636adf126a6696345bd2182d5b9c65eaa.png)

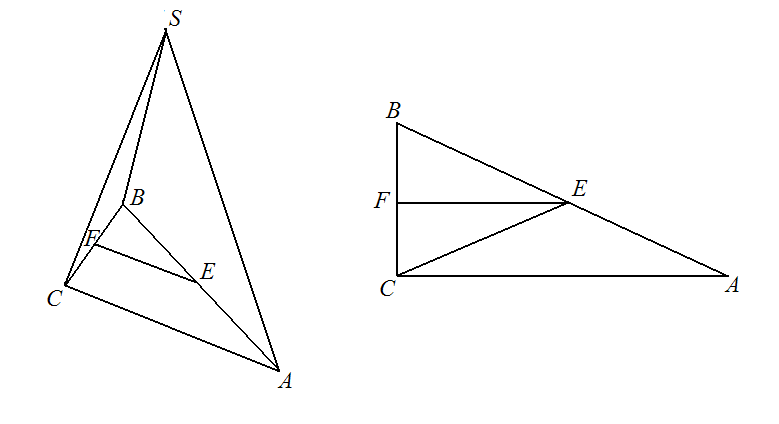

![\textbf{\underline{Zadanie 3.}}<br />
Rozwiązać równanie<br />
$$\displaystyle \sin^{10}x+\cos^{10}x=\frac{29}{16}\cos^{4}2x.$$<br />
\\ \\<br />
\textbf{\underline{Rozwiązanie}}<br />
Ze wzoru $a^5+b^2=(a+b)(a^4-a^3b+a^2b^2-ab^3+b^4)$:<br />
$$\sin^{10}x+\cos^{10}x=<br />
(\sin^{2}x+\cos^2x)(\sin^8x-\sin^6x\cos^2x+\sin^4x\cos^4x-\sin^2x\cos^6x+\cos^8x)=$$ $$=<br />
(\sin^8x+\cos^8x)-\sin^6x\cos^2x+\sin^4x\cos^4x-\sin^2x\cos^6x=$$ $$=<br />
(\sin^4x+\cos^4x)^2-2\sin^4x\cos^4x-\sin^6x\cos^2x+\sin^4x\cos^4x-\sin^2x\cos^6x=$$ $$=<br />
[(\sin^2x+\cos^2x)^2-2\sin^2x\cos^2x]^2-\sin^6x\cos^2x-\sin^4x\cos^4x-\sin^2x\cos^6x=$$ $$=<br />
\left(1-\frac{1}{2}\sin^22x\right)^2-\sin^2x\cos^2x\left(\sin^4x+\sin^2x\cos^2x+\cos^4x\right)=$$ $$=<br />
1-\sin^22x+\frac{1}{4}\sin^4 2x-\frac{1}{4}\sin^2 2x\left[(\sin^2x+\cos^2x)^2-\sin^2x\cos^2x\right]=$$<br />](/files/tex/d619225f6c78086c292a6e8b8070bc34b9a16cca.png)