Finał 2006 Rozwiązania

Wysłane przez dn w wt., 28/04/2015 - 05:23

<br /> \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół<br /> średnich - Matematyka} \centerline{Finał VII edycji - 24 czerwca 2006}<br /> \centerline{Przykładowe rozwiązania}<br />




\textbf{\underline{Zadanie 1.}}<br /> Rozwiązać równanie<br /> $$\left( \sqrt{1-\cos x}-\sin x\right) \left( \sin x+\cos x-1-\frac{1}{2}\sin 2x\right) =0.$$<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Dziedzina: $1-\cos x\geqslant 0$, stąd $x\in\mathbb{R}$.<br /> \\ Równanie jest równoważne:<br /> $$\sqrt{1-\cos x}-\sin x=0\quad\vee\quad \sin x+\cos x-1-\frac{1}{2}\sin 2x=0$$<br /> \\ Rozważmy najpierw pierwsze równanie:<br /> \begin{align*}<br /> \sqrt{1-\cos x}-\sin x & =0 \\<br /> \sqrt{1-\cos x} & =\sin x<br /> \end{align*}<br /> \\ Gdy $\sin x<0$, to otrzymujemy sprzeczność (lewa strona jest nieujemna, prawa zaś ujemna).<br /> \\ Niech więc $\sin x\geqslant 0$, czyli $\displaystyle x\in\bigcup_{k\in\mathbb{Z}}\left<2k\pi,\pi+2k\pi\right>$, podnosimy równanie stronami do kwadratu:<br /> \begin{align*}<br /> 1-\cos x &=\sin^2x\\<br /> 1-\cos x &=1-\cos^2x\\<br /> \cos^2x-\cos x &=0\\<br /> \cos x(\cos x-1) &=0\\<br /> \cos x=0\quad &\vee\quad\cos x=1<br /> \end{align*}<br /> \\ Powyższe dwa równania spełnione są dla dla $x=\frac{\pi}{2}+k\pi, x=2k\pi$, jednak po uwzględnieniu założenia $\sin x\geqslant 0$, otrzymujemy, że rozwiązaniami są następujące:<br /> $$x=\frac{\pi}{2}+2k\pi, x=2k\pi,\quad k\in\mathbb{Z}$$<br /> <br /> Zajmijmy się teraz drugim równaniem:<br /> \begin{align*}<br /> \sin x+\cos x-1-\frac{1}{2}\sin 2x &=0\\<br /> 2\sin x+2\cos x-2-\sin 2x &=0\\<br /> 2(\sin x+\cos x)-1-1-2\sin x\cos x &=0\\<br /> 2(\sin x+\cos x)-1-(\cos^2x+2\sin x\cos x+\sin^2x) &=0\\<br /> 2(\sin x+\cos x)-1-(\sin x+\cos x)^2 &=0\\<br /> -[(\sin x+\cos x)-1]^2 &=0\\<br /> \sin x+\cos x-1 &=0\\<br /> \sin x+\cos x &=1\\<br /> \frac{1}{\sqrt{2}}\sin x+\frac{1}{\sqrt{2}}\cos x &=\frac{1}{\sqrt{2}}\\<br /> \sin x\cos\frac{\pi}{4}+\cos x\sin\frac{\pi}{4} &=\frac{\sqrt{2}}{2}\\<br /> \sin\left(x+\frac{\pi}{4}\right) &=\frac{\sqrt{2}}{2}<br /> \end{align*}<br /> \begin{align*}<br /> x+\frac{\pi}{4}=\frac{\pi}{4}+2k\pi\quad &\vee\quad x+\frac{\pi}{4}=\frac{3\pi}{4}+2k\pi,\qquad k\in\mathbb{Z}\\<br /> x=2k\pi\quad &\vee\quad x=\frac{\pi}{2}+2k\pi<br /> \end{align*}<br /> \\ Reasumując odpowiedzią jest:<br /> $$x\in\bigcup_{k\in\mathbb{Z}}\left\{2k\pi,\frac{\pi}{2}+2k\pi\right\}.$$<br /> \\ \\<br /> \\ \\<br />

\textbf{\underline{Zadanie 2.}} Dany jest czworokąt ABCD wpisany w okrąg, którego przekątne AC i BD są wzajemnie prostopadłe i przecinają się w punkcie O. Przez ten punkt poprowadzono prostą prostopadłą do boku AD. Udowodnić, że prosta ta dzieli bok BC na połowy.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\ Przyjmijmy oznaczenia jak na rysunku:<br />

<br /> \\ Niech $\angle EOC=\alpha$.<br /> \\ Oczywiście wtedy $\angle AOP=\alpha$ (z kątów wierzchołkowych).<br /> \\ Z sumy miar kątów wewnętrznych w trójkącie $AOP$ otrzymujemy, że<br /> \\ $\angle PAO=90^{\circ}-\alpha$.<br /> \\ Z sumy miar kątów wewnętrznych w trójkącie $AOD$ otrzymujemy, że<br /> \\ $\angle ADO=\alpha$.<br /> \\ Kąty $\angle ADO$ oraz $\angle ACB$ są kątami wpisanymi opartymi na tym samym łuku, skąd<br /> $\angle ACB=\alpha$.<br /> \\ Stąd otrzymujemy, że trójkąty $OE'E, E'CE, OE''E,E''BE$ są trójkątami przystającymi (każdy ma kąty $\alpha, 90^{\circ},90^{\circ}-\alpha$ oraz parami wspólne boki), więc $|BE|=|EC|$.<br />

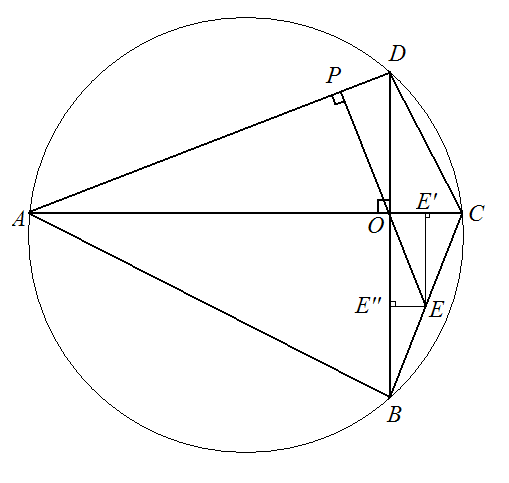
\textbf{\underline{Zadanie 3.}}<br /> Zbadać monotoniczność i ekstrema oraz narysować wykres funkcji<br /> $$ y=\left| f\left( x\right) \right|,$$<br /> jeżeli<br /> $$ f\left( x\right) =\lim_{n\rightarrow +\infty }\left[ x-x^{4}+x^{7}-\ldots +\left( -1\right) ^{n+1}x^{3n-2}\right].$$<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> $f(x)$ jest szeregiem geometrycznym o wyrazie pierwszym $a_1=x$ oraz ilorazie<br /> $q=-x^3$, by był to szereg zbieżny musi zachodzić $|q|<1$, czyli $|-x^3|<1$,<br /> $|x|<1$, $x\in(-1,1)$. Jest to nasza dziedzina.<br /> \\ Wtedy ze wzoru na sumę szeregu geometrycznego:<br /> $$f(x)=\frac{a_1}{1-q}=<br /> \frac{x}{1+x^3}$$<br /> \\ Narysujmy $y=f(x)$.<br /> \\ Zbadajmy granice na krańcach dziedziny:<br /> $$\lim_{x\to -1^+}f(x)=<br /> \lim_{x\to -1^+}\frac{x}{1+x^3}=<br /> \left[\frac{-1}{0^+}\right]=<br /> -\infty$$<br /> $$\lim_{x\to 1^-}f(x)=<br /> \lim_{x\to 1^-}\frac{x}{1+x^3}=<br /> \frac{1}{2}$$<br /> \\ Zatem w $x=-1$ istnieje asymptota pionowa prawostronna.<br /> <br /> Zbadajmy monotoniczność oraz ekstrema $f(x)$ (funkcja różniczkowalna w dziedzinie).<br /> $$f'(x)=\frac{1(1+x^3)-x(3x^2)}{(1+x^3)^2}=<br /> \frac{1+x^3-3x^3}{(1+x^3)^2}=<br /> \frac{-2x^3+1}{(1+x^3)^2}$$<br /> \\<br /> $$f'(x)=0$$<br /> $$\frac{-2x^3+1}{(1+x^3)^2}=0$$<br /> $$-2x^3+1=0$$<br /> $$-2x^3=-1$$<br /> $$x^3=\frac{1}{2}$$<br /> $$x=\frac{1}{\sqrt[3]{2}}$$<br /> \\<br /> $$f'(x)>0$$<br /> $$\frac{-2x^3+1}{(1+x^3)^2}>0$$<br /> $$-2x^3+1>0$$<br /> $$-2x^3>-1$$<br /> $$x^3<\frac{1}{2}$$<br /> $$x<\frac{1}{\sqrt[3]{2}}$$<br /> $$x\in\left(-1,\frac{1}{\sqrt[3]{2}}\right)$$<br /> <br /> Zatem funkcja $f(x)$ rośnie w przedziale $\displaystyle x\in\left(-1,\frac{1}{\sqrt[3]{2}}\right)$<br /> \\<br /> $$f'(x)<0$$<br /> $$\frac{-2x^3+1}{(1+x^3)^2}<0$$<br /> $$-2x^3+1<0$$<br /> $$-2x^3<-1$$<br /> $$x^3>\frac{1}{2}$$<br /> $$x>\frac{1}{\sqrt[3]{2}}$$<br /> $$x\in\left(\frac{1}{\sqrt[3]{2}},1\right)$$<br /> \\ Zatem funkcja $f(x)$ maleje w przedziale $\displaystyle x\in\left(\frac{1}{\sqrt[3]{2}},1\right)$.<br /> \\ Zatem $f(x)$ posiada ekstremum maksimum lokalne w $x=\frac{1}{\sqrt[3]{2}}$<br /> równe<br /> $$f\left(\frac{1}{\sqrt[3]{2}}\right)=<br /> \frac{\frac{1}{\sqrt[3]{2}}}{\frac{1}{2}+1}=<br /> \frac{\frac{1}{\sqrt[3]{2}}}{\frac{3}{2}}=<br /> \frac{2}{3\sqrt[3]{2}}$$<br /> \\ Szkic wykresu (po prawej stronie szkic wykresu $y=|f(x)|$.<br />

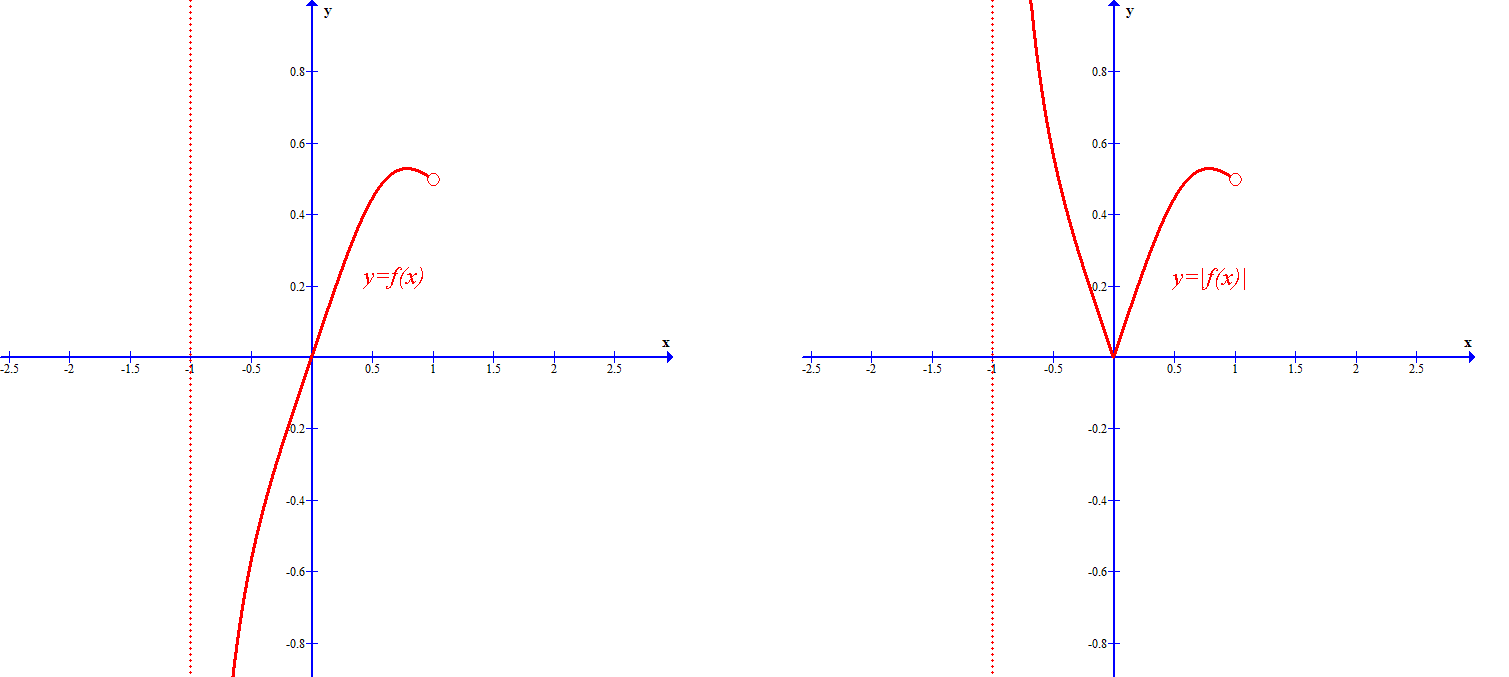
<br /> Monotoniczność funkcji $y=|f(x)|$ (wypiszemy największe przedziały,<br /> w których funkcja jest monotoniczna):<br /> \begin{itemize}<br /> \item funkcja $|f(x)|$ jest malejąca w przedziale $\left(-1,0\right>$ oraz<br /> w przedziale $\displaystyle\left<\frac{1}{\sqrt[3]{2}},1\right)$.<br /> \item funkcja $|f(x)|$ jest rosnąca w przedziale $\left<0,\frac{1}{\sqrt[3]{2}}\right>$.<br /> \item funkcja $|f(x)|$ posiada ekstremum minimum globalne dla $x=0$ równe $0$.<br /> \item funkcja $|f(x)|$ posiada ekstremum maksimum lokalne dla<br /> $\displaystyle x=\frac{1}{\sqrt[3]{2}}$ równe $\displaystyle\frac{2}{3\sqrt[3]{2}}$.<br /> \\ \\<br />

\textbf{\underline{Zadanie 4.}} Dane są trzy wzajemnie prostopadłe odcinki $OA$, $OB$, $OC$ o długościach odpowiednio<br /> $a$, $b$, $c$. Obliczyć odległość punktu $O$ od płaszczyzny trójkąta $ABC$.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br />

<br /> Z tw. Pitagorasa w trójkątach $OAC$, $OAB$, $OBC$ otrzymamy, że:<br /> $$|AB|=\sqrt{a^2+b^2}$$<br /> $$|AC|=\sqrt{a^2+c^2}$$<br /> $$|BC|=\sqrt{b^2+c^2}$$<br /> \\ Niech $\angle BAC=\alpha$.<br /> \\ Z tw. cosinusów w trójkącie $ABC$:<br /> $$|BC|^2=|AB|^2+|AC|^2-2|AB|\cdot|AC|\cos\alpha$$<br /> $$b^2+c^2=a^2+b^2+a^2+c^2-2\sqrt{a^2+b^2}\sqrt{a^2+c^2}\cos\alpha$$<br /> $$\cos\alpha=\frac{a^2}{\sqrt{a^2+b^2}\sqrt{a^2+c^2}}$$<br /> \\ Z jedynki trygonometrycznej (ponieważ $\alpha\in(0,\pi)$, to $\sin\alpha>0$):<br /> $$\sin\alpha=\sqrt{1-\cos^2\alpha}=<br /> \sqrt{1-\frac{a^4}{(a^2+b^2)(a^2+c^2)}}=$$ $$=<br /> \sqrt{\frac{a^4+a^2b^2+a^2c^2+b^2c^2-a^4}{(a^2+b^2)(a^2+c^2)}}=$$ $$=<br /> \frac{\sqrt{a^2b^2+a^2c^2+b^2c^2}}{\sqrt{a^2+b^2}\sqrt{a^2+c^2}}$$<br /> \\ Zatem pole trójkąta $ABC$:<br /> $$P_{ABC}=\frac{1}{2}|AB|\cdot |AC|\cdot\sin\alpha=<br /> \frac{1}{2}\sqrt{a^2+b^2}\sqrt{a^2+c^2}\cdot \frac{\sqrt{a^2b^2+a^2c^2+b^2c^2}}{\sqrt{a^2+b^2}\sqrt{a^2+c^2}}=$$ $$=<br /> \frac{1}{2}\sqrt{a^2b^2+a^2c^2+b^2c^2}$$<br /> \\<br /> \\ Obliczymy teraz objętość $OABC$ na dwa sposoby, niech $x$ oznacza szukaną odległość punktu $O$ od płaszczyzny trójkąta $ABC$:<br /> $$V_{OABC}=V_{OABC}$$<br /> $$\frac{1}{3}P_{OAB}\cdot c=\frac{1}{3}P_{ABC}\cdot x$$<br /> $$\frac{1}{3}\cdot\frac{1}{2}abc=\frac{1}{3}\cdot\frac{1}{2}\sqrt{a^2b^2+a^2c^2+b^2c^2}\cdot x$$<br /> $$x=\frac{abc}{\sqrt{a^2b^2+a^2c^2+b^2c^2}}$$<br /> \\ \\<br />

\textbf{\underline{Zadanie 5.}} Spośród liczb naturalnych od 1 do 1200 losujemy bez zwracania dwie liczby: m i n. Jakie jest prawdopodobieństwo zdarzenia, że liczba<br /> $$\displaystyle 2\left( mn\right) ^{2}+m^{2}$$<br /> jest podzielna przez $12$? Wynik podać z dokładnością do $0,01$.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> Niech $\Omega$ oznacza przestrzeń wszystkich zdarzeń elementarnych, polegających na wylosowaniu bez zwracania dwóch liczb $m,n$ spośród liczb naturalnych od $1$ do $1200$, oczywiście<br /> $$|\Omega|=1200\cdot 1199$$<br /> \\ Niech $A$ oznacza zbiór tych zdarzeń elementarnych dla których liczba $M=2(mn)^2+m^2$ jest podzielna przez $12$.<br /> Zauważmy, że $M=2(mn)^2+m^2=m^2(2n^2+1)$.<br /> \\ Ponieważ liczba $M$ musi być podzielna przez $12$ oraz liczba $2n^2+1$ jest<br /> zawsze nieparzysta, to musi być $4|m^2$, czyli $2|m$.<br /> \\ Dodatkowo zauważmy, że gdy $3|n$, to liczba $2n^2+1$ nie jest podzielna przez $3$,<br /> a gdy $3\not |n$, to $2n^2+1$ jest podzielna przez $3$ (korzystamy z faktu, że kwadrat liczby, która nie jest podzielna przez $3$ daje resztę $1$ przy dzieleniu przez $3$).<br /> \\ Zatem, by liczba $M$ była podzielna przez $12$, to $2|m$ oraz $3|m$ lub $3\not | n$.<br /> \\ Inaczej, by liczba $M$ była podzielna przez $12$, to $6|m$ lub $2|m$ i $3\not |n$.<br /> \\ Niech $A_1$ - oznacza te sytuacje, że $6|m$, niech $A_2$ oznacza te sytuacje, że $2|m$ i $3\not | n$.<br /> <br /> Chcemy zatem obliczyć prawdopodobieństwo:<br /> $$P(A)=P(A_1\cup A_2)=<br /> P(A_1)+P(A_2)-P(A_1\cap A_2)$$<br /> \\<br /> \\ Oczywiście $|A_1|=200\cdot 1199$ (mamy $200$ możliwości wyboru liczby $m$, a następnie $1199$ możliwości wyboru liczby $n$).<br /> \\ By obliczyć $|A_2|$ zobaczmy, że mamy $200$ liczb podzielnych przez $6$ oraz<br /> $400$ liczb parzystych, które nie dzielą się przez $3$. Dodatkowo mamy $400$ liczb podzielnych przez $3$, wiec mamy $800$ liczb, które nie dzielą się przez $3$.<br /> Gdy wybierzemy $m$ jako liczbę podzielną przez $6$ (200 możliwości), to wtedy mamy $800$ możliwości wybrania liczby $n$.<br /> \\ Gdy wybierzemy $m$ jako liczbę parzystą, która nie dzieli się przez $6$ (400 możliwości), to wtedy liczbę $n$ możemy wybrać już na $800-1=799$ sposobów. Zatem:<br /> \\ $|A_2|=200\cdot 800+400\cdot 799$.<br /> \\<br /> \\ $A_1\cap A_2$ oznacza $6|m$ oraz $3\not |n$, tych sytuacji jest $200\cdot 800$.<br /> \\ Wracając do liczenia prawdopodobieństwa:<br /> $$P(A)=P(A_1\cup A_2)=<br /> P(A_1)+P(A_2)-P(A_1\cap A_2)=$$ $$=<br /> \frac{200\cdot 1199+200\cdot 800+400\cdot 799-200\cdot 800}{1200\cdot 1199}=$$ $$=<br /> \frac{200\cdot 1199+400\cdot 799}{1200\cdot 1199}\approx<br /> 0.39$$<br /> \\ \\<br />

<br /> \centerline{\bf Za rozwiązanie każdego zadania można uzyskać<br /> maksymalnie 20 punktów}<br />