Finał 2014 Rozwiązania

Wysłane przez dn w śr., 19/11/2014 - 23:36

<br /> \centerline{POWSZECHNY KONKURS INTERNETOWY dla uczniów szkół<br /> średnich - Matematyka} \centerline{Finał XV edycji - 12 kwietnia<br /> 2014}<br /> \centerline{Przykładowe rozwiązania}<br />




<br /> \textbf{\underline{Zadanie 1.}} Wykazać, że każda liczba naturalna $n$ spełnia następującą nierówność<br /> \[ \frac{1 \cdot 2 - 1}{2!} + \frac{2 \cdot 3 -1}{3!} + \frac {3<br /> \cdot 4 -1}{4!} + \ldots + \frac{n \cdot (n+1)-1}{(n+1)!}< 2 -<br /> \frac{2}{(n+1)!}\]<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\<br /> Zauważmy, że<br /> $$\frac{n(n+1)-1}{(n+1)!}=\frac{n(n+1)}{(n-1)!n(n+1)}-\frac{1}{(n+1)!}=<br /> \frac{1}{(n-1)!}-\frac{1}{(n+1)!}.$$<br /> Przekształćmy lewą stronę nierówności:<br /> $$\frac{1\cdot 2}{2!}+\frac{2\cdot 3-1}{3!}+\frac{3\cdot 4-1}{4!}+\ldots+\frac{(n-1)n-1}{n!}+\frac{n\cdot (n+1)-1}{(n+1)!}=$$<br /> $$=\frac{1}{0!}-\frac{1}{2!}+\frac{1}{1!}-\frac{1}{3!}+\frac{1}{2!}-\frac{1}{4!}+\frac{1}{3!}-\frac{1}{5!}+\ldots+\frac{1}{(n-2)!}-\frac{1}{n!}+\frac{1}{(n-1)!}-\frac{1}{(n+1)!}=$$<br /> $$=\frac{1}{0!}+\frac{1}{1!}-\frac{1}{n!}-\frac{1}{(n+1)!}$$<br /> Nasza nierówność przyjmuje postać:<br /> $$1+1-\frac{1}{n!}-\frac{1}{(n+1)!}<2-\frac{2}{(n+1)!}$$<br /> Przekształcamy równoważnie nierówność:<br /> $$-\frac{1}{n!}-\frac{1}{(n+1)!}<-\frac{2}{(n+1)!}$$<br /> \\ Mnożymy przez $-(n+1)!$:<br /> $$(n+1)+1>2$$<br /> $$n>0$$<br /> Jest to oczywiście prawda, więc początkowa nierówność jest również prawdziwa.<br />




<br /> \textbf{\underline{Zadanie 2.}} Rozwiązać równanie<br /> \[<br /> \sin^4\frac{\pi}{8}+\sin^4\frac{3\pi}{8}+\sin^4\frac{5\pi}{8}+\sin^4\frac{7\pi}{8}=(\sin<br /> x+\cos x)^2<br /> \]<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\<br /> Przekształćmy lewą stronę równania:<br /> $$\sin^4\frac{\pi}{8}+\sin^4\frac{3\pi}{8}+\sin^4\frac{5\pi}{8}+\sin^4\frac{7\pi}{8}=$$<br /> \\ Ze wzoru $\sin\alpha=\sin(\pi-\alpha)$:<br /> $$=\sin^4\frac{\pi}{8}+\sin^4\frac{3\pi}{8}+\sin^4\frac{3\pi}{8}+\sin^4\frac{\pi}{8}=<br /> 2\left(\sin^4\frac{\pi}{8}+\sin^4\frac{3\pi}{8}\right)=$$<br /> \\ Ze wzoru $\sin\alpha=\cos\left(\frac{\pi}{2}-\alpha\right)$:<br /> $$=<br /> 2\left(\sin^4\frac{\pi}{8}+\cos^4\frac{\pi}{8}\right)=$$<br /> \\ Z tożsamości $a^2+b^2=(a+b)^2-2ab$:<br /> $$=<br /> 2\left[\left(\sin^2\frac{\pi}{8}+\cos^2\frac{\pi}{8}\right)^2-2\sin^2\frac{\pi}{8}\cos^2\frac{\pi}{8}\right]=<br /> 2\left[1^2-\frac{1}{2}\left(2\sin\frac{\pi}{8}\cos\frac{\pi}{8}\right)^2\right]=$$<br /> \\ Ze wzoru $\sin 2\alpha=2\sin\alpha\cos\alpha$:<br /> $$=<br /> 2\left(1-\frac{1}{2}\sin^2\frac{\pi}{4}\right)=<br /> 2\left(1-\frac{1}{2}\cdot\frac{1}{2}\right)=<br /> 2\cdot\frac{3}{4}=<br /> \frac{3}{2}$$<br /> \\ Wracając do początkowego równania:<br /> $$\frac{3}{2}=\left(\sin x+\cos x\right)^2$$<br /> $$\frac{3}{2}=\sin^2x+2\sin x\cos x+\cos^2x$$<br /> $$\frac{3}{2}=1+\sin 2x$$<br /> $$\sin 2x=\frac{1}{2}$$<br /> $$2x=\frac{\pi}{6}+2k\pi\quad\vee\quad 2x=\pi-\frac{\pi}{6}+2k\pi,\quad k\in\mathbb{Z}$$<br /> $$x=\frac{\pi}{12}+k\pi\quad\vee\quad x=\frac{5\pi}{12}+k\pi,\quad k\in\mathbb{Z}$$<br />




<br /> \textbf{\underline{Zadanie 3.}} Kawałek drutu o długości 22 cm zgięto pod kątem prostym \linebreak w<br /> losowo wybranym punkcie. Następnie zgięto drut w dwóch \linebreak<br /> punktach, tak aby utworzyła się ramka w kształcie prostokąta<br /> \linebreak o obwodzie 22 cm.<br /> Jakie jest prawdopodobieństwo, ze pole obszaru<br /> ograniczonego ramką nie przekracza 24 cm$^2$?<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\<br /> Niech $x$ - długość krótszego odcinka po pierwszym zgięciu. \\ Oczywiście $x\in\left(0,11\right)$.<br /> \\ Wtedy boki powstałego prostokąta mają długości $x,11-x$, więc jego pole to $P(x)=x(11-x)$.<br /> \\ Chcemy, by zachodziło:<br /> $$P(x)\leqslant 24$$<br /> $$x(11-x)\leqslant 24$$<br /> $$11x-x^2\leqslant 24$$<br /> $$x^2-11x+24\geqslant 0$$<br /> $$(x-3)(x-8)\geqslant 0$$<br /> $$x\in\left(-\infty;3\right>\cup\left<8;\infty\right)$$<br /> \\ Zawężając do dziedziny: $x\in\left(0,3\right>\cup\left<8,11\right)$.<br /> \\ Przejdźmy do policzenia prawdopodobieństwa.<br /> \\ $\Omega$ - zdarzenie polegające na wybraniu losowego $x$ z przedziału $(0,11)$ (przestrzeń wszystkich zdarzeń), długość przedziału wynosi oczywiście $11$.<br /> \\ $A$ - zdarzenie polegające na wybraniu losowego $x$ z przedziału $\left(0,3\right>\cup\left<8,11\right)$, długość przedziału wynosi oczywiście $3+3=6$.<br /> \\ Szukane prawdopodobieństwo zdarzenia $A$ będzie równe stosunkowi długości odpowiednich przedziałów, stąd u nas $\displaystyle P(A)=\frac{6}{11}$<br />




<br /> \textbf{\underline{Zadanie 4.}} Dany jest czworokąt $ABCD$ wpisany w okrąg. Dwusieczne kątów<br /> \linebreak tego czworokąta przecinają okrąg w punktach $E$, $F$,<br /> $G$, $H$. \linebreak Udowodnić, że suma kwadratów odległości<br /> dowolnego punktu $P$ \linebreak z tego okręgu od punktów $E$, $F$,<br /> $G$, $H$ jest stała, tzn. nie zależy \linebreak od wyboru tego<br /> punktu na okręgu.<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\<br />

<br /> Niech $\angle DAB=2\alpha$, $\angle ABC=2\beta$, $\angle BCD=2\gamma$, $\angle CDA=2\delta$. Z warunków wpisania czworokąta w okrąg otrzymujemy równości $2\alpha+2\gamma=\pi$ oraz $2\beta+2\delta=\pi$, stąd $\displaystyle \alpha+\gamma=\frac{\pi}{2}$, $\displaystyle \beta+\delta=\frac{\pi}{2}$.<br /> \\ Na mocy własności kątów wpisanych opartych na tych samych łukach otrzymujemy:<br /> $$\angle FGH=\angle FGC+\angle CGH=\angle FDC+\angle HBC=\delta+\beta=\frac{\pi}{2}$$<br /> $$\angle GHE=\angle GHB+\angle BHE=\angle GCB+\angle BAE=\gamma+\alpha=\frac{\pi}{2}$$<br /> \\ Wynika stąd, że czworokąt $EFGH$ jest prostokątem.<br />

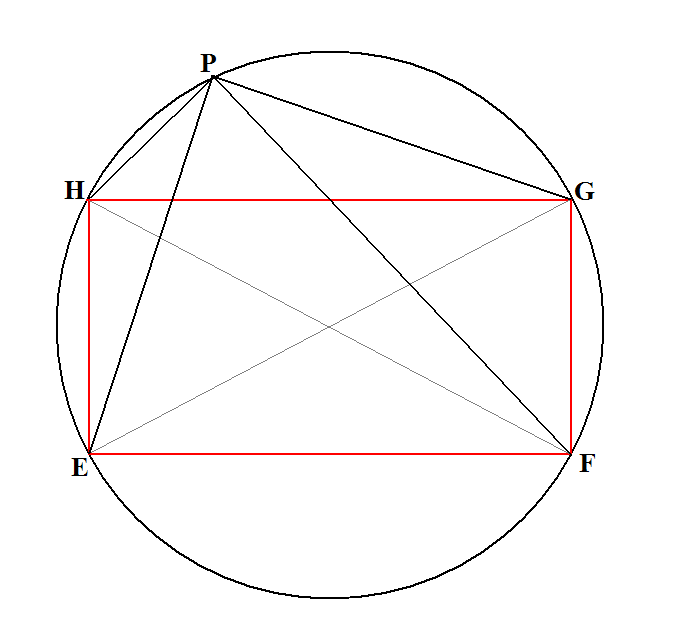
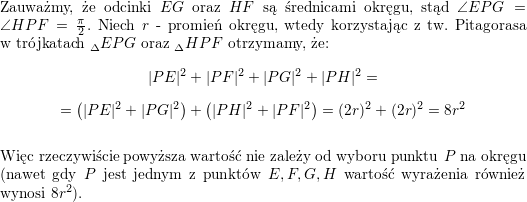
<br /> Zauważmy, że odcinki $EG$ oraz $HF$ są średnicami okręgu, stąd $\angle EPG=\angle HPF=\frac{\pi}{2}$. Niech $r$ - promień okręgu, wtedy korzystając z tw. Pitagorasa w trójkatach $ _{\Delta}EPG$ oraz $ _{\Delta}HPF$ otrzymamy, że:<br /> $$|PE|^2+|PF|^2+|PG|^2+|PH|^2=$$<br /> $$=\left(|PE|^2+|PG|^2\right)+\left(|PH|^2+|PF|^2\right)=(2r)^2+(2r)^2=8r^2$$<br /> \\ Więc rzeczywiście powyższa wartość nie zależy od wyboru punktu $P$ na okręgu (nawet gdy $P$ jest jednym z punktów $E,F,G,H$ wartość wyrażenia również wynosi $8r^2$).<br />




<br /> \textbf{\underline{Zadanie 5.}} Niech $n$ będzie liczbą naturalną. Ze zbioru $M=\{1,2, \ldots,<br /> 3n\}$ \linebreak wybieramy w losowy sposób jego podzbiór $X$.<br /> Rozważmy \linebreak<br /> następujące zdarzenia:\\<br /> $A$ - wylosowany zbiór $X$ nie zawiera żadnej pary liczb naturalnych<br /> $x$, $y$, \linebreak dla których $n$ jest dzielnikiem liczby $|y-x|$, \\<br /> $B$ - wylosowany zbiór $X$ jest taki, że z jego elementów mozna<br /> utworzyć dokładnie trzy, niekoniecznie rozłączne, pary liczb<br /> naturalnych $x$, $y$, \linebreak dla których $n$ jest dzielnikiem<br /> liczby $|y-x|$.\\<br /> Znaleźć najmniejszą liczność zbioru $M$, dla której spełniona jest<br /> \linebreak następująca nierówność<br /> \[2^6\cdot P(B) > 43 \cdot n \cdot P(A). \]<br /> \\ \\<br /> \textbf{\underline{Rozwiązanie}}<br /> \\ \\<br /> Niech $\Omega$ oznacza zbiór wszystkich zdarzeń elementarnych, czyli zbiór wszystkich podzbiorów zbioru $\mathcal{M}$.<br /> \\<br /> Korzystamy z tego, że ilość podzbiorów zbioru $m$-elementowego wynosi $2^m$, stąd w naszym wypadku:<br /> $$|\Omega|=2^{3n}=8^n$$<br /> \\<br /> \\ Zdarzenia przychylne zdarzeniu $A$.<br /> \\ By warunki zadania zostały spełnione w wylosowanym zbiorze nie może być więcej niż jednej liczby z każdego z $n$ następujących zbiorów:<br /> $$\{1,n+1,2n+1\}$$<br /> $$\{2,n+2,2n+2\}$$<br /> $$\vdots$$<br /> $$\{n,2n,3n\}$$<br /> \\ Stąd:<br /> $$|A|=4\cdot 4\cdot\ldots\cdot 4=4^n$$<br /> \\ (ponieważ z każdego zbioru możemy wybrać jedną z trzech liczb, lub nie wybrać żadnej, stąd $4$ możliwości).<br /> \\ \\<br />


<br /> Zdarzenia przychylne zdarzeniu $B$.<br /> \\ By warunki zadania zostały spełnione musimy ALBO wybrać trzy elementy z jednego z wypisanego wcześniej zbioru - bo wtedy mamy trzy pary: jedna $k,n+k$, druga $k,2n+k$, trzecia $n+k,2n+k$ ALBO wybrać po dwa elementy z trzech różnych wcześniej wypisanych zbiorów, a resztę liczb możemy dobrać w analogiczny jak przy zdarzeniu $A$ sposób - czyli dobieramy do wybranych przez nas liczb co najwyżej jedną liczbę z każdego z pozostałych zbiorów. Druga możliwość jest również uwzględniona nawet dla $n<3$, bo wtedy $\displaystyle {n\choose 3}=0$ (nie jest możliwa).<br /> \\ Stąd:<br /> $$|B|={n\choose 1}{3\choose 3}4^{n-1}+{n\choose 3}{3\choose 2}{3\choose 2}{3\choose 2}4^{n-3}$$<br /> \\<br /> \\ Rozwiązujemy więc nierówność:<br /> $$2^6P(B)>43nP(A)$$<br /> $$64\cdot\frac{n4^{n-1}+\frac{n(n-1)(n-2)}{6}\cdot 3\cdot 3\cdot 3\cdot 4^{n-3}}{8^n}>43n\cdot\frac{4^n}{8^n}$$<br /> \\ Mnożymy przez $8^n$, dzielimy przez $n$, dzielimy przez $4^n$:<br /> $$64\left(\frac{1}{4}+\frac{(n-1)(n-2)\cdot 3\cdot 3}{2\cdot 4^3}\right)>43$$<br /> $$16+\frac{9(n-1)(n-2)}{2}>43$$<br /> $$32+9(n-1)(n-2)>86$$<br /> $$32+9(n^2-3n+2)>86$$<br /> $$9n^2-27n+18+32>86$$<br /> $$9n^2-27n-36>0$$<br /> $$n^2-3n-4>0$$<br /> $$(n+1)(n-4)>0$$<br /> \\ Dzielimy przez $n+1>0$:<br /> $$n-4>0$$<br /> $$n>4$$<br /> \\ Stąd najmniejsza liczba $n$ to $5$, więc szukana ilość elementów zbioru $\mathcal{M}$ to $15$, jak XV edycja konkursu.<br />


<br /> \centerline{\bf Za rozwiązanie każdego zadania można uzyskać<br /> maksymalnie 20 punktów}<br />